Algorithm¶
Neural architecture search¶
AutoML is a family of techniques and algorithms seeking to automatically solve supervised learning tasks. Recently, researchers in AutoML have investigated whether we can automate learning the structure of a neural network for a given dataset, automating a task that requires significant domain expertise. This subdomain known as neural architecture search has seen advances in the state-of-the-art using reinforcement learning [Zoph et al. ‘17], evolutionary strategies [Real et al., ‘17], and gradient-based methods [Liu et al., ‘18] to learn neural network substructures. However, in these papers, the high-level structure of the network generally remains user defined.
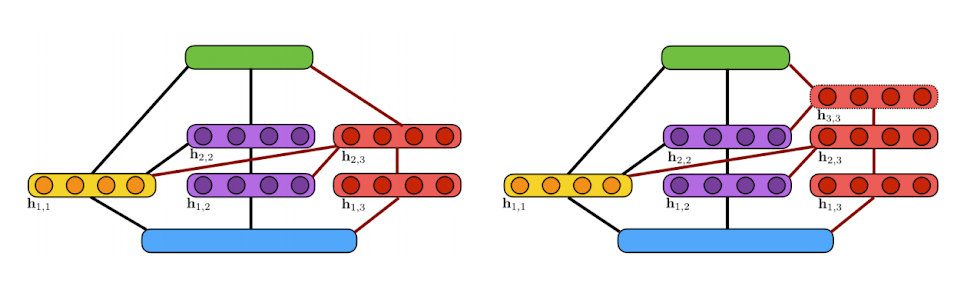 Two candidate ensembles
Two candidate ensembles
This illustration shows the algorithm’s incremental construction of a fully-connected neural network. The input layer is indicated in blue, the output layer in green. Units in the yellow block are added at the first iteration while units in purple are added at the second iteration. Two candidate extensions of the architecture are considered at the third iteration (shown in red): (a) a two-layer extension; (b) a three-layer extension. Here, a line between two blocks of units indicates that these blocks are fully-connected.
Neural networks are ensembles¶
Ensembles of neural networks have shown remarkable performance in domains such as natural language processing, image recognition, and many others. The two composing techniques are interesting in their own rights: ensemble techniques have a rich history and theoretical understanding, while neural networks provide a general framework for solving complex tasks across many domains at scale.
Coincidentally, an ensemble of neural networks whose outputs are linearly combined is also a neural network. With that definition in mind, we seek to answer the question: Can we learn a neural network architecture as an ensemble of subnetworks? And can we adaptively learn such an ensemble with fewer trainable parameters and that performs better than any single neural network trained end-to-end?
Adaptive architecture search¶
Our algorithm for performing adaptive neural architecture search is AdaNet [Cortes et al., ICML ‘17], which iteratively grows an ensemble of neural networks while providing learning guarantees. It is adaptive because at each iteration the candidate subnetworks are generated and trained based on the current state of the neural network.
We show this algorithm can in fact learn a neural network (ensemble) that achieves state of the art results across several datasets. We also show how this algorithm is complementary with the neural architecture search research mentioned earlier, as it learns to combine these substructures in a principled manner to achieve these results.
The AdaNet algorithm¶
The AdaNet algorithm works as follows: a generator iteratively creates a set of candidate base learners to consider including in the final ensemble. How these base learners are trained is left completely up to the user, but generally they are trained to optimize some common loss function such as cross-entropy loss or mean squared error. At every iteration, the trained base learners then evaluated on their ability to minimize the AdaNet objective $F$, and the best one is included in the final ensemble.
$$\begin{aligned} &F\left ( w \right ) = \frac{1}{m} \sum_{i=0}^{N-1} \Phi \left (\sum_{j=0}^{N-1}w_jh_j(x_i), y_i \right ) + \sum_{j=0}^{N-1} \left (\lambda r(h_j) + \beta \right )\left | w_j \right |\ &\text{where }w_j \text{ is the weight of model } j \text{’s contribution to the ensemble,}\ &h_j \text{ is model } j,\ &\Phi \text{ is the loss function,}\ &r(h_j) \text{ is model } j\text{’s complexity, and}\ &\lambda \text{ and } \beta \text{ are tunable hyperparameters.} \end{aligned}$$
For every iteration after the first, the generator can generate neural networks based on the current state of the ensemble. This allows AdaNet to create complex structures or use advanced techniques for training candidates so that they will most significantly improve the ensemble. For an optimization example, knowledge distillation [Hinton et al., ‘15] is a technique that uses a teacher network’s logits as the ground-truth when computing the loss of a trainable student network, and is shown to produce students that perform better than a identical network trained without. At every iteration, we can use the current ensemble as a teacher network and the candidates as students, to obtain base learners that perform better, and significantly improve the performance of the final ensemble.